Curriculum and Approach

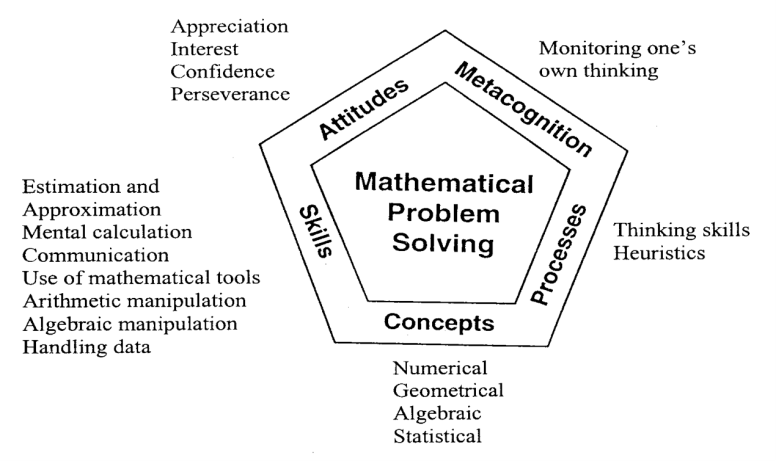
Our school aligns our mathematics curricular approach with the broad aims of mathematics education in Singapore to enable students to:

acquire and apply mathematical concepts and skills;
develop cognitive and metacognitive skills through a mathematical approach to problem solving; and
develop positive attitudes towards mathematics.

Singapore Mathematics Framework

We achieve this by designing our math programme into 3 phases, with a focus on building strong foundation in the subject right from the start.

Si Ling Mathematics 6 year Programme

Phase	Level	Objectives
PHASE 1: Laying the Foundation	P1 and P2	Develop interest and enjoyment in learning mathematics. Develop a deep understanding of concepts.
PHASE 2: Building up the Skills and Processes	P3 and P4	Build confidence in using mathematics. Develop reasoning, communication and problem solving skills.
PHASE 3: Sharpening the Mathematical Skills and Processes	P5 and P6	Apply reasoning, communication and problem solving skills. Prepare for PSLE.

Some of our common approaches:

1. Concrete-Pictorial-Abstract (CPA) Approach

The Concrete-Pictorial-Abstract Approach (CPA) is used in the teaching of mathematics. Lessons are designed using the CPA sequence to foster deeper understanding of mathematical concepts.

Concrete is the “doing” stage. During this stage, students use concrete objects to model problems.

Pictorial is the “seeing” stage. Here, visual representations of concrete objects are used to model problems.

Abstract is the “symbolic” stage, where children use abstract symbols to model problems.

2. BEST Approach to Problem Solving

The Polya’s 4-step problem solving process was adapted and we called it the BEST approach to problem solving. This approach focus on metacognition which is thinking about thinking, refers to the awareness of, and the ability to control one’s thinking processes. This approach provides a structured development to pupils’ thinking process as they solve the word problem.

3. Model Method

The model method is used for effective mathematics learning and problem solving. The drawing of model helps our pupils understand complex mathematical word problems. It helps pupils to develop and enhance pupils’ mathematical thinking and problem solving in the early years of mathematical education.

4. Improving Confidence and Achievement in Numeracy (ICAN)

In Si Ling, we embarked on the ICAN programme by the Ministry of Education (Curriculum Planning and Development Division) to enhance the teaching and learning of mathematics. ICAN uses intervention strategies guided by research to address 4 key issues namely learning gaps, language, motivation and memory.

The ICAN principles

Routines and Norms
Diagnosis and Feedback
Practice and Review
Explicit and Direct Instructions
Scaffolding and Progression
Key Ideas and their Connections
Communication and Reasoning
Confidence and Motivation